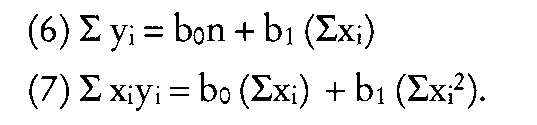Zweistufige Kleinste-Quadrate-Schätzung

In der Statistik und Ökonometrie ist die zweistufige Kleinste-Quadrate-Schätzung bzw. zweistufige KQ-Schätzung (ZSKQ-Schätzung), auch zweistufige Methode der kleinsten Quadrate (englisch Two Stage Least Squares, kurz: TSLS oder 2SLS) genannt, ein durch den Ökonometriker Henri Theil entwickeltes Schätzverfahren mit beschränkter Information. Bei diesem zweistufigen Verfahren werden als erstes die endogenen (d. h. die mit der Störgröße korrelierten Variablen) auf alle exogenen Variablen der Gleichung und alle Instrumente regressiert. Als zweites werden die so gewonnenen geschätzten Werte für die endogenen Regressoren, die als Linearkombination exogener Variablen nicht mit dem Störterm korreliert sind, dann ins Ursprungsmodell eingesetzt und das so entstehende neue Modell geschätzt. Der zweistufige Kleinste-Quadrate-Schätzer kann als Instrumentvariablenschätzer interpretiert werden. Die ZSKQ-Schätzung ist nach der gewöhnlichen Methode der kleinsten Quadrate an zweiter Stelle bei der Schätzung linearer Gleichungen in der angewandten Ökonometrie.

Das Verfahren

Gegeben sei ein typisches multiples lineares Regressionsmodell ${\displaystyle \mathbf {y} =\mathbf {X} {\boldsymbol {\beta }} {\boldsymbol {\varepsilon }}}$ (wahres Modell), mit ${\displaystyle {\boldsymbol {\beta }}}$ dem ${\displaystyle (p\times 1)}$-Vektor der unbekannten Regressionsparameter, der ${\displaystyle (n\times p)}$-Versuchsplanmatrix ${\displaystyle \mathbf {X} }$, dem ${\displaystyle (n\times 1)}$-Vektor der abhängigen Variablen ${\displaystyle \mathbf {y} }$ und dem ${\displaystyle (n\times 1)}$-Vektor der Störgrößen ${\displaystyle {\boldsymbol {\varepsilon }}}$. Der verallgemeinerte Kleinste-Quadrate-Schätzer (VKQ-Schätzer) kann auf unterschiedliche Art und Weise ausgedrückt werden. Jede dieser Ausdrucksweisen hat ihre eigene Interpretation. Eine bekannte Spezifikation ist die sogenannte zweistufige Kleinste-Quadrate-Schätzung, die von Henri Theil entwickelt wurde. Für die Herleitung des zweistufigen Kleinste-Quadrate-Schätzers lässt sich der verallgemeinerte Kleinste-Quadrate-Schätzer ${\displaystyle {\tilde {\boldsymbol {\delta }}}_{i}}$ wie folgt ausdrücken:

${\displaystyle {\tilde {\boldsymbol {\delta }}}_{i}=(\mathbf {Z} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {Z} _{i})^{-1}\mathbf {Z} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y} _{i}={\begin{pmatrix}\mathbf {Y} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {Y} _{i}&\mathbf {Y} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {X} _{i}\\\\\mathbf {X} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {Y} _{i}&\mathbf {X} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {X} _{i}\\\\\end{pmatrix}}^{-1}\cdot {\begin{pmatrix}\mathbf {Y} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y} _{i}\\\\\mathbf {X} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y} _{i}\\\\\end{pmatrix}}}$

Die reduzierte Form lautet ${\displaystyle \mathbf {Y} =\mathbf {X} \mathbf {\Pi } \mathbf {V} }$. Die ${\displaystyle i}$-te Gleichung der reduzierten Form kann wie folgt partitioniert werden:

${\displaystyle [\mathbf {y} _{i}\;\;\mathbf {Y} _{i}\;\;\mathbf {Y} _{i}^{*}]=\mathbf {X} [\pi _{i}\;\;\mathbf {\Pi } \;\;\mathbf {\Pi } _{i}^{*}] [\mathbf {v} _{i}\;\;\mathbf {V} _{i}\;\;\mathbf {V} _{i}^{*}]}$,

wobei ${\displaystyle \mathbf {y} _{i}}$ der ${\displaystyle (T\times 1)}$-Vektor der ${\displaystyle i}$-ten gemeinsam abhängigen Variablen ist, ${\displaystyle \mathbf {Y} _{i}^{*}}$ die anderen gemeinsam abhängigen Variablen in der ${\displaystyle i}$-ten Gleichung beinhaltet, ${\displaystyle \mathbf {Y} _{i}^{*}}$ die ${\displaystyle (T\times m_{i}^{*})}$-Matrix der gemeinsam abhängigen Variablen ist, die nicht in der ${\displaystyle i}$-ten Gleichung auftauchen, und ${\displaystyle [\pi _{i}\;\;\mathbf {\Pi } \;\;\mathbf {\Pi } _{i}^{*}]}$ die partitionierte Matrix von Koeffizienten der reduzierten Form ist. Der Kleinste-Quadrate-Schätzer von ${\displaystyle \mathbf {\Pi } _{i}}$ lautet ${\displaystyle {\hat {\mathbf {\Pi } }}_{i}=(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {Y} _{i}}$ und daher gilt durch Zuhilfenahme der Prädiktionsmatrix ${\displaystyle \mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {Y} _{i}=\mathbf {X} {\hat {\mathbf {\Pi } }}_{i}={\hat {\mathbf {Y} }}_{i}=\mathbf {Y} _{i}-{\hat {\mathbf {V} }}_{i}}$, wobei ${\displaystyle {\hat {\mathbf {Y} }}_{i}}$ die ${\displaystyle (T\times (m_{i}-1))}$-Matrix der vorhergesagten Werte von ${\displaystyle \mathbf {Y} _{i}}$ ist. Durch die Tatsache, dass ${\displaystyle (\mathbf {X} ^{\top }\mathbf {X} )^{-1}(\mathbf {X} ^{\top }\mathbf {X} )=\mathbf {I} }$, kann man auch schreiben:

${\displaystyle {\tilde {\boldsymbol {\delta }}}_{i}={\begin{pmatrix}\mathbf {Y} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }(\mathbf {X} ^{\top }\mathbf {X} )^{-1}(\mathbf {X} ^{\top }\mathbf {X} )\mathbf {Y} _{i}&\mathbf {Y} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {X} _{i}\\\\\mathbf {X} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {Y} _{i}&\mathbf {X} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {X} _{i}\\\\\end{pmatrix}}^{-1}\cdot {\begin{pmatrix}\mathbf {Y} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y} _{i}\\\\\mathbf {X} _{i}^{\top }\mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y} _{i}\\\\\end{pmatrix}}}$

bzw.

${\displaystyle {\tilde {\boldsymbol {\delta }}}_{i}={\begin{pmatrix}{\hat {\mathbf {Y} }}_{i}^{\top }{\hat {\mathbf {Y} }}_{i}&{\hat {\mathbf {Y} }}_{i}^{\top }\mathbf {X} _{i}\\\\\mathbf {X} _{i}^{\top }{\hat {\mathbf {Y} }}_{i}&\mathbf {X} _{i}^{\top }\mathbf {X} _{i}\\\\\end{pmatrix}}^{-1}\cdot {\begin{pmatrix}{\hat {\mathbf {Y} }}_{i}^{\top }\mathbf {y} _{i}\\\\\mathbf {X} _{i}^{\top }\mathbf {y} _{i}\\\\\end{pmatrix}}}$

Wenn man ${\displaystyle {\hat {\mathbf {Z} }}_{i}=[{\hat {\mathbf {Y} }}_{i}\;\;\mathbf {X} _{i}]}$ definiert, dann kann der zweistufige Kleinste-Quadrate-Schätzer wie folgt spezifiziert werden

${\displaystyle {\tilde {\boldsymbol {\delta }}}_{i}=({\hat {\mathbf {Z} }}_{i}^{\top }{\hat {\mathbf {Z} }}_{i})^{-1}{\hat {\mathbf {Z} }}_{i}^{\top }\mathbf {y} _{i}}$.

Literatur

• George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee. Introduction to the Theory and Practice of Econometrics. 2. Auflage. John Wiley & Sons, New York/ Chichester/ Brisbane/ Toronto/ Singapore 1988, ISBN 0-471-62414-4.

Einzelnachweise

Weblinks

• Springer Gabler Verlag, Gabler Wirtschaftslexikon, Stichwort: Kleinstquadratemethode, zweistufige